Jiwon Park

Starting now

Updated:

0. Introduction

Dataset: Graduate Admission 2, Admission_Predict.csv
Kaggle Dataset

이 데이터셋은 대학원 지원자의 정보(GRE, TOEFL 점수 등)와 대학의 등급을 기반으로 각 지원자가 합격할 확률(Chance of Admit)을 기록한 데이터입니다. 변수를 살펴보면:

  • Series No.: 데이터의 인덱스 변수.
  • GRE Scores ( out of 340 ): GRE 점수
  • TOEFL Scores ( out of 120 ): TOEFL 점수
  • University Rating ( out of 5 ): 대학의 등급을 나타내지만 졸업한 대학의 등급인지, 지원하는 대학의 등급인지 알 수 없습니다. 1~5의 값을 갖는데 높을수록 입학이 어려운 학교인지 낮을수록 어려운지 알 수 없습니다.
  • Statement of Purpose Strength ( out of 5 ): PoS가 얼마나 강력한지 나타내는 변수입니다.
  • Letter of Recommendation Strength ( out of 5 ): 추천레터가 얼마나 강력한지 나타내는 변수입니다.
  • Undergraduate GPA ( out of 10 ): 대학교 성적입니다. 10점 만점인 것으로 보아 4.0 만점의 점수와 4.5 만점의 점수의 스케일을 맞춘 것 같습니다.
  • Research Experience ( either 0 or 1 ): 연구 경험 보유 여부를 나타냅니다.
  • Chance of Admit ( ranging from 0 to 1 ): 합격할 확률을 나타내는 변수로, 이번 모델의 target variable입니다.


1. EDA

1-1 모델 구축에 필요하지 않은 변수

첫번째 변수인 Serial No.는 단순히 데이터의 순서를 나타내기 때문에 모델 구축에 필요하지 않습니다. 따라서 input variable index는 2~8번 입니다.

library(psych) 
library(ggplot2)
library(corrplot)
library(moments)
library(xlsx)
library(pROC)
library(ROCR)

# Load dataset
admission <- read.csv("Admission_Predict.csv")
View(admission)
input_idx <- c(2,3,4,5,6,7,8)
target_idx <- 9

view


1-2 입력 변수들의 단변량 통계량과 Boxplot

입력 변수의 단변량 통계량입니다.

df <- data.frame(matrix(ncol=5, nrow=0))
colnames(df) <- c("variable", "mean", "sd", "skew", "kurtosis")
for (i in 2:8){
  a <- describe(admission[,i])
  df <- rbind(df,data.frame(variable = colnames(admission[i]),mean = a$mean,sd= a$sd , skew=a$skew ,kurtosis= a$kurtosis))
}
df

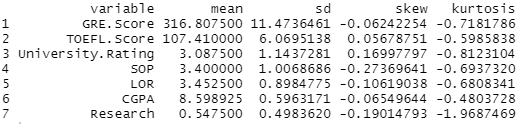
dstats


다음은 boxplot입니다.

#Boxplot for each variable
ggplot(admission, aes(x="", y=GRE.Score)) +geom_boxplot(fill='#E69F00', color="black")+theme_classic()
ggplot(admission, aes(x="", y=TOEFL.Score)) +geom_boxplot(fill='#E69F00', color="black")+theme_classic()
ggplot(admission, aes(x="", y=University.Rating)) +geom_boxplot(fill='#E69F00', color="black")+theme_classic()
ggplot(admission, aes(x="", y=SOP)) +geom_boxplot(fill='#E69F00', color="black")+theme_classic()
ggplot(admission, aes(x="", y=LOR)) +geom_boxplot(fill='#E69F00', color="black")+theme_classic()
ggplot(admission, aes(x="", y=CGPA)) +geom_boxplot(fill='#E69F00', color="black")+theme_classic()
ggplot(admission, aes(x="", y=Research)) +geom_boxplot(fill='#E69F00', color="black")+theme_classic()

boxplots

독립변수의 단변량 통계량과 boxplot을 살펴본 결과, 정규분포를 따른다고 할 수 있는 변수들은 다음과 같습니다.

  • GRE Score: Box plot과 skewness로부터 대칭성을 확인했습니다. 단, kurtosis가 -0.7181로 정규분포가 갖는 kurtosis인 3보다는 작은 값이었습니다. 정규분포보다 약간 납작한 모양일 것이라고 예상합니다.
  • TOEFL Score: Box plot이 대칭이고, skewness가 매우 작으므로 대칭일 것입니다. GRE와 마찬가지로 kurtosis가 음수기 때문에 정규분포보다는 아래로 눌린 모양일 것입니다.
  • CGPA: Box plot과 skewness를 살펴보았을 때, 데이터가 대칭이라고 생각했습니다. 위의 두 변수와 마찬가지로 negative kurtosis를 가지므로 정규분포보다 뭉툭한 모양일 것입니다.


1-3 이상치 조건 정의와 제거

위의 Boxplot들을 봤을 때, GRE score, TOEFL score, University Rating, SOP, 그리고 Research는 이상치가 발견되지 않았습니다. LOR과 CGPA는 이상치로 보이는 점이 발견되었지만, 실제 데이터를 보고 아웃라이어가 아니라고 판단했습니다.

1-4 Scatterplot과 Correlation plot

독립변수들의 조합에 대해 Scatterplot과 correaltion plot을 그려 변수 간 상관관계를 파악하였습니다.

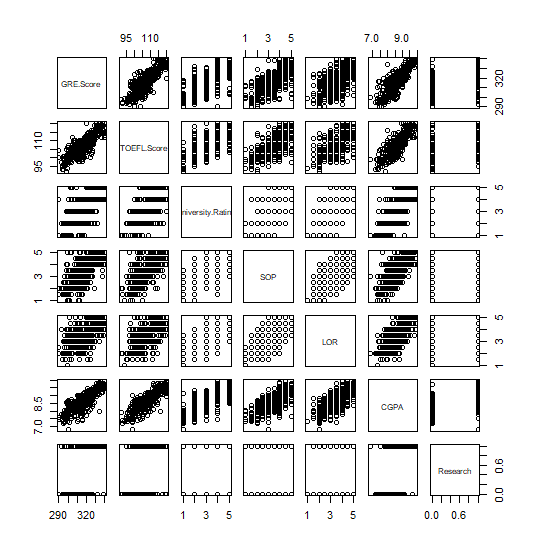
#Q4. Scatterplot
pairs(admission[c(2,3,4,5,6,7,8)])

scatterplot

#correlation plot
add_cor <- cor(admission[c(2,3,4,5,6,7,8)], method=c("spearman"))
add_cor
corrplot(add_cor)

correlation

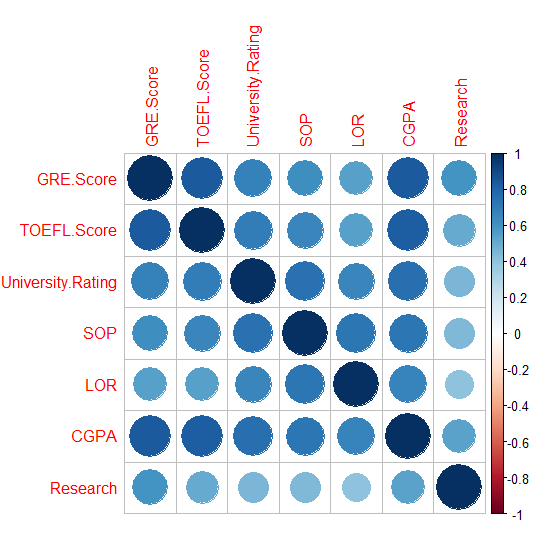
correlation plot

  • Correlation plot으로부터 GRE Score와 TOEFL Score, 그리고 GRE Score와 CGPA가 가장 큰 상관관계를 가지는 것을 알 수 있었습니다.
  • Scatter plot에서도 양의 상관관계가 뚜렷하게 드러났습니다. 시험 성적이 좋은 학생이 다른 시험이나 학점에서도 좋은 점수를 받기 때문으로 추측됩니다.
  • CGPA는 GRE Score 뿐만 아니라 TOEFL Score, University Rating, SOP 등 다른 변수들과도 강한 양의 상관관계를 갖는 것으로 보입니다.

2. 전처리

2-1 종속변수 변환

종속변수인 Chance of Admit은 0~1 사이의 확률로 저장되어 있습니다. Classification 문제로 만들기 위해 cutoff를 0.8로 설정하여 0.8을 초과하면 1 (positive class), 초과하지 않으면 0 (negative class)의 값을 갖는 binary target variable로 변환했습니다.

#change chance_of_admission variable into binary variable
chance_of_Ad <- rep(0, length(admission[,9]))
chance_of_Ad[which(admission[,9] > 0.8)] <- 1
chance_of_Ad
admission[,9] <- chance_of_Ad


2-2 입력변수 Normalization

다음으로, 입력변수들에 대해 normalization을 수행했습니다. 이론적으로는 logistic regression에서 normalization이 필수는 아니지만, 입력변수끼리 값의 범위가 크게 차이 날 경우 R에서 계산하며 rounding error가 발생할 수 있기 때문입니다.

# Conduct the normalization
admission_input <- admission[,input_idx]
admission_input <- scale(admission_input, center = TRUE, scale = TRUE)
admission_target <- admission[,target_idx]
admission_data <- data.frame(admission_input, admission_target)


2-3 데이터셋 분할

Seed를 92735로 설정하여 전체 데이터셋을 70%의 학습 데이터와 30%의 테스트 데이터로 분할했습니다.

# Split the data into the training/validation sets
set.seed(92735)
trn_idx <- sample(1:nrow(admission_data), round(0.7*nrow(admission_data)))
admission_trn <- admission_data[trn_idx,]
admission_tst <- admission_data[-trn_idx,]



3. Modeling

3-1 Model 구축

위에서 준비한 데이터를 사용하여 Logistic Regression 모델을 구축했습니다.

# Train the Logistic Regression Model with all variables
full_lr <- glm(admission_target ~ ., family=binomial, admission_trn)
summary(full_lr)


결과는 다음과 같습니다.

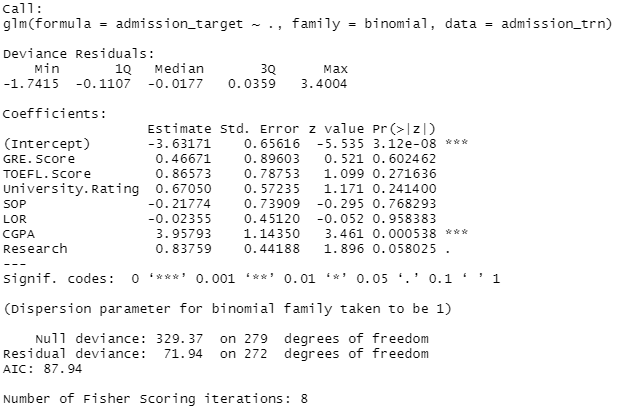
full_result

  • 유의수준 0.1에서 Chance of Admit에 유의미하게 영향을 주는 변수들을 파악하기 위해 p-value를 살펴보았습니다. Coefficient의 값이 0이라는 귀무가설을 기각하기 위해서는 p-value가 0.1보다 낮아야 합니다.
  • P-value가 0.1보다 작은, 즉 유의미한 변수들은 CGPA와 Research였습니다.


3-2 Test 데이터셋에 대한 예측과 Confusion Matrix

Test 데이터셋에 대하여 예측을 수행하고 Confusion Matrix를 생성했습니다. Cutoff는 0.8로 설정했습니다.

# Test the logistic regression model and calculate confusion matrix
lr_response <- predict(full_lr, type = "response", newdata = admission_tst)
lr_target <- admission_tst$admission_target
lr_predicted <- rep(0, length(lr_target))
lr_predicted[which(lr_response > 0.8)] <- 1
cm_full <- table(lr_target, lr_predicted)
cm_full

cm

모델이 TEST 데이터셋에 대해 합격을 제대로 예측한 경우가 29번, 불합격을 제대로 예측한 경우가 77번, 합격인데 불합격이라고 잘못 예측한 경우가 11번, 불합격인데 합격이라고 잘못 예측한 경우가 3번이었습니다.


3-3 Performance measure

위의 Confusion matrix를 바탕으로 True Positive Rate, True Negative Rate, False Positive Rate, False Negative Rate, Simple Accuracy, Balanced Correction Rate, F1-Measure를 구했습니다.

# Performance Evaluation Function -----------------------------------------
perf_eval2 <- function(cm){
  # True positive rate: TPR (Recall)
  TPR <- cm[2,2]/sum(cm[2,])
  # True negative rate: TNR
  TNR <- cm[1,1]/sum(cm[1,])
  # False positive rate: FPR
  FPR <- cm[2,1]/sum(cm[2,])
  # False negative rate: FNR
  FNR <- cm[1,2]/sum(cm[1,])
  # Simple Accuracy
  ACC <- (cm[1,1]+cm[2,2])/sum(cm)
  # Balanced Correction Rate
  BCR <- sqrt(TPR*TNR)
  # Precision
  PRE <- cm[2,2]/sum(cm[,2])
  # F1-Measure
  F1 <- 2*TPR*PRE/(TPR+PRE)
  
  return(c(TPR,TNR, FPR, FNR, ACC, BCR, PRE, F1))
}

# Initialize the performance matrix1
perf_mat <- matrix(0, 1, 8)
colnames(perf_mat) <- c("TPR","TNR", "FPR", "FNR", "ACC", "BCR", "PRE", "F1")
rownames(perf_mat) <- "Logstic Regression"

perf_mat[1,] <- perf_eval2(cm_full)
perf_mat

TPR | TNR | FPR | FNR | ACC | BCR | PRE | F1 –|–|–|–|–|–|–|– 0.725|0.963|0.275 |0.038 |0.883|0.835|0.906|0.806

  • 단순 Accuracy는 0.883이었습니다.
  • TPR은 0.725로, 실제 합격자 중 72.5%가 제대로 identified 되었음을 의미합니다. TPR이 Accuracy보다 낮은 것은 불합격 데이터가 합격 데이터에 비해 많았기 때문으로 예상합니다.
  • Precision은 0.906으로, 모델에 의해 합격이라고 예측된 사람들 중 90.6%가 실제 합격자였음을 의미합니다.
  • TNR은 0.963이었습니다. 실제 불합격자 중 96.3%가 제대로 identified 되었음을 나타냅니다.


단순 accuracy만으로는 모델의 performance를 정확히 평가할 수 없습니다. 데이터의 불균형이 심한 경우 한 클래스를 제대로 예측하지 못하더라도 다른 클래스를 제대로 예측한 횟수가 많아서 높게 계산될 수 있기 때문입니다. 따라서 이러한 단점을 보완한 BCR과 F1 measure도 살펴보아야 합니다.

  • BCR은 TNR과 TPR을 곱한 값에 루트를 씌운 값입니다. 따라서 class imbalance가 있을 때 TNR이나 TPR이 작게 나온다면 전체 값이 작아지게 됩니다.
  • F1은 Precision과 Recall의 가중평균으로, FP와 FN을 함께 고려합니다.
  • BCR은 0.835였고 F1은 0.806이었습니다. 모두 높은 값을 가지므로 이 모델은 좋은 performance를 낸다고 할 수 있습니다.


3-4 AUROC

Random seed를 변경해가며 학습과 테스트를 5회 반복했습니다. 각 테스트에 대해 ROCR 라이브러리를 사용해 ROC 그래프를 그리고 직접 AUROC를 산출했습니다.

seed_num <- c(92735, 12345, 23456, 34567, 45678)
for (i in seed_num){
  set.seed(i)
  trn_idx <- sample(1:nrow(admission_data), round(0.7*nrow(admission_data)))
  admission_trn <- admission_data[trn_idx,]
  admission_tst <- admission_data[-trn_idx,]
  
  # Train the Logistic Regression Model with all variables
  full_lr <- glm(admission_target ~ ., family=binomial, admission_trn)
  lr_response <- predict(full_lr, type = "response", newdata = admission_tst)
  lr_target <- admission_tst$admission_target
  pred <- prediction(lr_response, lr_target)
  roc <- performance(pred,"tpr","fpr")
  plot(roc,colorize=TRUE)
  
  
  x <- lr_response
  y <- lr_target
  x1 = x[y==1]; n1 = length(x1); 
  x2 = x[y==0]; n2 = length(x2);
  r = rank(c(x1,x2))  
  auc = (sum(r[1:n1]) - n1*(n1+1)/2) / n1 / n2
  print(auc)
  
}

Seed가 달라질 때마다 training set과 testing set이 달라져 매번 다른 ROC가 그려지고, 다른 AUROC가 계산되었습니다. roc


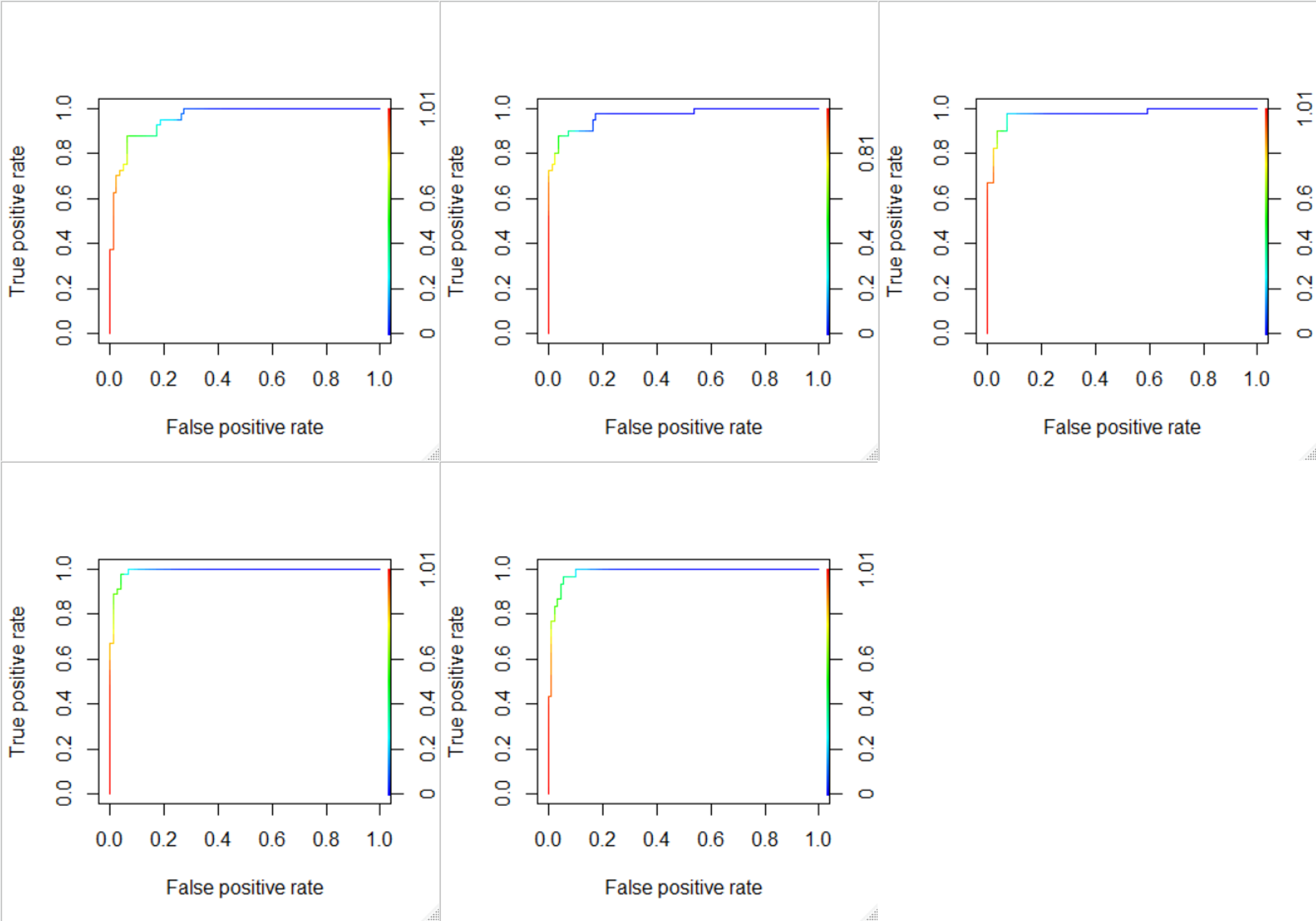
산출한 AUROC는 다음과 같습니다. | Seed | AUROC | |–|–| |92735 | 0.9581 | |12345 | 0.9678| |23456|0.9724| |34567|0.9922| |45678|0.9855|


5개 AUROC의 평균을 계산해보니 0.9752였습니다.

sum(0.958125, 0.9678125, 0.9724596, 0.9922963, 0.9855556)/5

False Positive Rate가 0이고, True Positive Rate가 1인 커브가 가장 이상적이므로, 이상적인 AUROC값은 1입니다. 랜덤하게 예측했을 때는 커브가 대각선으로 그려지므로 AUROC 값은 0.5가 된다.

  • 평균 AUROC가 0.9752로 1에 매우 가까운 수치입니다. 따라서 이 모델은 좋은 classifier라고 할 수 있습니다.
  • ROC 커브로부터 최적의 cut-off 값도 찾아낼 수 있습니다. 왼쪽 위 모서리에 가까울수록 FPR은 0에, TPR은 1에 가깝습니다. 왼쪽 위 모서리에 가장 가까운 커브의 색깔을 살펴보면 대부분 노란색과 초록색이 섞여있습니다. 커브 오른쪽의 index를 보면 노란색과 초록색은 0.6 ~ 0.7 정도를 나타내므로, cut-off를 0.6 ~ 0.7로 설정하는 것이 타당합니다.



4. 보완할 점

  • Class imbalance 확인해서 upsampling, undersampling 고려하기
  • performance evaluation 함수 대신 r에서 제공하는 confusion matrix 기능 사용해서 값 비교하기
  • 범주형 변수 EDA 더 알아보기
  • Coefficient 값 해석하기 - odds ratio 내용 추가
  • logistic regression이 만족해야할 가정은?
  • logistic regression의 장단점은? 어떤 경우 사용하는 것이 효과적인지?

You may also enjoy

2022년 1월 회고

January 31 2022

올해에는 매달 월말에 회고를 남기려고 한다. 나중에 읽어보면 도움도 되고 재밌을 것 같다.