[R] Multiple Linear Regression으로 부동산 가격 예측하기

Introduction

Dataset: House Sales in King County, USA, kc_house_data.csv
Kaggle dataset

House sales 데이터는 미국 King County에서 2014년 5월부터 2015년 5월까지 거래된 주택에 대한 정보를 나타냅니다. 각 변수에 대한 설명은 Kaggle 페이지의 Column 항목을 통해 확인할 수 있습니다. 이 중 세 번째 항목인 price가 MLR 모형의 target variable입니다.

1. EDA

1-1 모델 구축에 필요하지 않은 변수

Id, date, zipcode 변수는 MLR 모형 구축을 위해 필요하지 않습니다.

• ID는 서로 다른 집을 식별하는 코드일 뿐 의미가 없습니다.
• Zipcode는 지역을 구분하는 숫자입니다.

library(psych) 
library(ggplot2)
library(corrplot)
library(moments)

house <- read.csv("kc_house_data.csv")
head(house)

1-2 전처리가 필요한 변수

date는 팔린 날짜 뒤에 T000000이 붙어있어 그대로 사용할 수 없습니다.

• date변수를 연, 월, 일로 쪼개 house_soldyr, house_soldmnth, house_solddate라는 새로운 변수에 각각 저장했습니다

#Split house sold date into year, month, and date
house_soldyr <- as.numeric(substr(house[,2], 1, 4))
house_soldmnth <- as.numeric(substr(house[,2], 5, 6))
house_solddate <- as.numeric(substr(house[,2], 7, 8))
#Q1. Eliminate useless variable and add sold date
house1 <- cbind(house[,-c(1,2,17)], house_soldyr, house_soldmnth, house_solddate)

1-2 입력 변수들의 단변량 통계량과 Boxplot

개별 입력 변수의 단변량 통계량입니다.

#save mean, standard deviation, skewness, kurtosis in df
df <- data.frame(matrix(ncol=5, nrow=0))
colnames(df) <- c("variable", "mean", "sd", "skew", "kurtosis")
for (i in 1:21){
  a <- describe(house1[,i])
  df <- rbind(df,data.frame(variable = colnames(house1[i]),mean = a$mean,sd= a$sd , skew=a$skew ,kurtosis= a$kurtosis))
}
df

1-3 이상치 조건 정의와 제거

위의 Boxplot들을 봤을 때, 가운데 박스에서 점점 멀어질수록 이상치 값이 드물게 나타남을 알 수 있었습니다.

• e.g., Sqft_above변수의 Boxplot에서 90% percentile보다 큰 값들이 꽤 가깝게 몰려 있고, 더 커질수록 이상치가 드물어졌습니다.

단순히 90% percentile를 초과하는 값을 이상치로 정의하기에는 제거되는 관측치 수가 너무 크다고 생각해 이상치를 [(Q1-3IQR), (Q3+3IQR)로 정의했습니다.

이에 해당하는 객체들을 데이터셋에서 제거했습니다. 단, waterfront와 같이 0과 1로 이루어진 binary변수, yr_built처럼 이상치가 존재하지 않는 변수는 이상치를 제거하지 않았습니다.

#Q3. Remove Outliers
for (i in c(2,3,4,5,11,12,15,16,17,18)){
  house1 <- house1[house1[,i] > quantile(house1[,i], .25) - 3*IQR(house1[,i]) & 
                     house1[,i] < quantile(house1[,i], .75) + 3*IQR(house1[,i]), ] #rows
}

1-4 Scatterplot과 Correlation plot

수치형 변수들의 조합에 대해 Scatterplot과 correaltion plot을 그려 변수 간 상관관계를 파악하였습니다.

#Q4. Scatterplot
pairs(house1[c(2,3,4,5,6,9,10,11,12,13,14,15)])

#correlation plot
house_cor <- cor(house1[c(2,3,4,5,6,8,9,10,11,12,13,14,15,16,17,18)], method=c("spearman"))
house_cor
corrplot(house_cor)

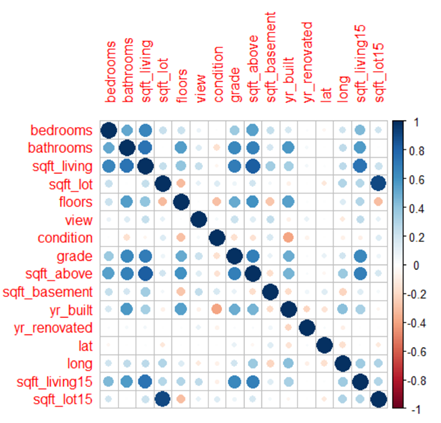
• 이로부터 sqft_lot15와 sqft_lot의 상관관계가 가장 높음을 알 수 있습니다. Sqft_lot15는 2015년의 lot size고, sqft_lot은 이전 lot size입니다. 리모델링을 하지 않았다면 lot size가 동일할 것이므로 이렇게 상관관계가 높게 나왔다고 생각합니다.
• Sqft_living15와 Sqft_living도 높은 상관관계가 있었습니다.
• Sqft_above와 Sqft_living역시 큰 상관관계가 있었습니다. Sqft_above는 지하를 제외한 집의 size이므로 livingroom size가 크면 sqft_above도 큰 값을 가지게 됩니다.
• Grade와 sqft_living도 큰 양의 상관관계가 있었습니다.

전처리

연속형 변수를 factor형 변수로 변형했습니다. 전체 데이터셋을 70%의 학습 데이터와 30%의 테스트 데이터로 분할했습니다.

##Continuous variables to factor variables 
house1$house_soldyr <- as.factor(house1$house_soldyr)
house1$house_soldyr
house1$house_soldmnth <- as.factor(house1$house_soldmnth)
house1$house_solddate <- as.factor(house1$house_solddate)
house1$waterfront <- as.factor(house1$waterfront)

#Split the data into the training/validation sets
nHome <- nrow(house1)
nVar <- ncol(house1)
house_trn_idx <- sample(1:nHome, round(0.7*nHome))
house_trn_data <- house1[house_trn_idx,]
house_val_data <- house1[-house_trn_idx,]

Modeling

모든 변수를 사용하여 MLR 모델을 구축했습니다.

# Train the MLR
mlr_house <- lm(price ~ ., data = house_trn_data)
mlr_house
summary(mlr_house)
plot(mlr_house)

결과는 다음과 같습니다.

Adjusted R2값은 0.6949였습니다. 이는 데이터가 비교적 선형성을 띄고 있고, 모델 구축에 사용한 변수들로 전체 변동의 69%를 설명할 수 있음을 나타냅니다.

모델 가정 검정

Ordinary Least Square 방식의 솔루션은 residual이 independent하며 평균이 0이고 분산이 constant한 정규분포를 따라야 한다는 가정이 있습니다.

가정을 만족하는지 알아보기 위해 Residual plot과 Q-Q Plot을 그렸습니다.

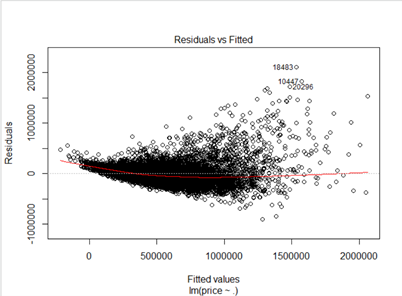
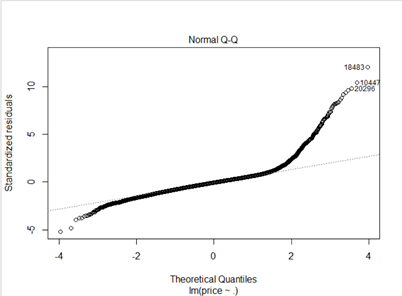
Residual Plot을 보았을 때, 잔차가 특정한 패턴 없이 골고루 퍼져있어야 합니다. 하지만 이 plot의 경우, 잔차가 깔때기 모양으로 점점 퍼져 나가는 것을 볼 수 있습니다. 따라서 잔차가 독립이라는 가정을 만족하기 힘들 것으로 보입니다. Normal QQ plot으로부터는 정규성을 확인할 수 있습니다. 비록 오른쪽 끝 부분에서 점들이 y=x 선과 많이 멀어지기는 했으나, 2의 근처에서 멀어지기 시작했으므로 대부분 정규성을 만족한다고 할 수 있습니다.

실제 그래프를 그렸습니다.

# normality test of residuals
house_resid <- resid(mlr_house)

m <- mean(house_resid)
std <- sqrt(var(house_resid))

hist(house_resid, density=20, breaks=50, prob=TRUE, 
     xlab="x-variable", main="normal curve over histogram")

curve(dnorm(x, mean=m, sd=std), 
      col="darkblue", lwd=2, add=TRUE, yaxt="n")

skewness(house_resid)
kurtosis(house_resid)

결과는 다음과 같습니다.

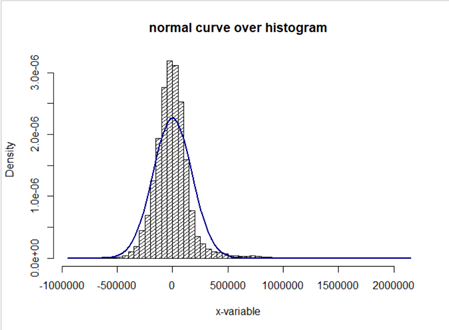
정규분포처럼 bell-shape이지만 정규분포보다 뾰족함을 알 수 있습니다.

유의미한 변수 파악

유의수준 0.01에서 모형 구축에 통계적으로 유의미한 변수들을 파악하기 위해 개별 변수의 p-value를 살펴보았습니다. P-value가 0.01보다 낮다는 것은 coefficient의 값이 0이라는 귀무가설을 기각할 수 있는 것이므로 변수가 유의미함을 나타내기 때문입니다. P-value가 0.01보다 낮은 변수들은 다음과 같았습니다. 변수들의 coefficient 값이 양수라면 해당 변수가 한 단위 증가할 때, price가 coefficient만큼 증가한다는 것이므로 양의 상관관계를 갖고, 음수라면 한 단위 증가할 때마다 price가 그만큼 감소하므로 음의 상관관계를 갖습니다. 양의 상관관계를 갖는 변수들은 bathrooms, sqft_living, waterfront 등이었고, 음의 상관관계를 갖는 변수들은 bedrooms, sqft_loft 등이었습니다.

변수	Coefficient	P-value
bedrooms	-2.941e+04	< 2e-16v
bathrooms	3.409e+04	< 2e-16
sqft_living	1.183e+02	< 2e-16
sqft_lot	-2.433e+00	0.000711
waterfront1	4.475e+05	< 2e-16
view	4.730e+04	< 2e-16
condition	3.380e+04	< 2e-16
grade	1.050e+05	< 2e-16
sqft_above	2.800e+01	9.16e-08
yr_built	-2.475e+03	< 2e-16
yr_renovated	3.254e+01	7.05e-15
lat	5.707e+05	< 2e-16
long	-8.153e+04	1.28e-08
sqft_living15	4.934e+01	< 2e-16
house_soldyr2015	5.605e+04	1.56e-07

Test 데이터셋의 MAE, MAPE, RMSE

Test 데이터셋에 대하여 MAE, MAPE, RMSE를 계산했습니다.

# Performance evaluation function for regression --------------------------
perf_eval_reg <- function(tgt_y, pre_y){
  
  # RMSE
  rmse <- sqrt(mean((tgt_y - pre_y)^2))
  # MAE
  mae <- mean(abs(tgt_y - pre_y))
  # MAPE
  mape <- 100*mean(abs((tgt_y - pre_y)/tgt_y))
  
  return(c(rmse, mae, mape))
  
}

perf_mat <- matrix(0, nrow = 1, ncol = 3)

# Initialize a performance summary
rownames(perf_mat) <- c("kc_house")
colnames(perf_mat) <- c("RMSE", "MAE", "MAPE")
perf_mat


#Q7. Performance Measure
mlr_house_haty <- predict(mlr_house, newdata = house_val_data)

perf_mat[1,] <- perf_eval_reg(house_val_data$price, mlr_house_haty)
perf_mat

• MAE는 절대평균오차로 실제값과 예측값의 차이의 절댓값의 평균입니다. 이 모델의 MAE는 113890.7로 평균적으로 이만큼의 차이가 있었음을 알 수 있습니다. MAE는 차이의 크기는 제공하지만 y의 스케일에 상관없이 계산됩니다.
• 이를 보완한 것이 MAPE로 이 모델의 값은 24.40328이었습니다. 이는 y값에 비해 얼마나 차이가 있었는지를 나타내는 것입니다.
• RMSE는 168912.4로, 차이의 제곱의 평균에 루트를 씌운 것입니다. 부호의 영향을 제거하기 위해 제곱을 했기 때문에 MAE보다 큰 값이 계산되었습니다.

(여기에선 performance matrix를 따로 만들어서 계산했는데, 다음에는 R에서 제공하는 함수를 이용하려고 합니다.)